久保拓弥「データ解析のための統計モデリング入門」を読み終えたので、次はCameron Davidson-Pilon著、玉木徹訳の「Pythonで体験するベイズ推論」(GitHubリポジトリ) をJuliaとMamba.jlでモデリングしていきたいと思う。
まず例題1.4.1の「メッセージ数に変化はあるか?」をやってみる。
元のノートブックはこれ。
JuliaでCSVファイルをhttps上から取るには、パッケージ HTTP , CSV をインポートして
r = HTTP.request("GET", "https://git.io/vXTVC");
count_data = CSV.read(IOBuffer(r.body), header=["messages"])
とすれば良い。
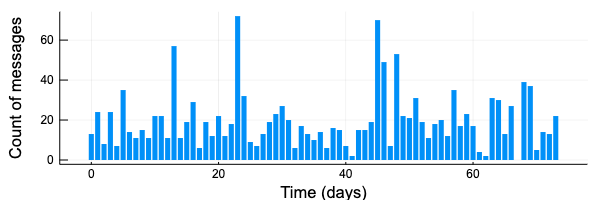
Plotsでプロットすると下のような感じ。Juliaはインデックスが1から始まるので、x軸を 0:N-1 にしておく。
N = length(count_data.messages)
bar(0:N-1, count_data.messages, label = "", size = [600, 200],
linecolor = :transparent,
xlabel = "Time (days)", ylabel = "Count of messages")
\( i \) 日目のメッセージ数 \( C_i \) がポアソン分布 \( \text{Poisson}(\lambda) \) に従い、\( \lambda \) の値が突然ある日 \( \lambda \) で変わる日があるとする。\( \tau < \lambda \) のとき \( \lambda = \lambda_1, \tau \ge \lambda \) の時 \( \lambda=\lambda_2 \)とする。
この \( \tau, \lambda_1, \lambda_2 \) 推定する。\( \lambda_1, \lambda_2 \) の事前分布は指数分布 \( \text{Exp}(\alpha) \) とする。ここでαは計数データの平均の逆数である。\( \tau \) の事前分布は一様分布とする。
Mambaでモデリングするときに注意しないといけないのは、PyMCと分布のパラメトライズが一部異なるところである。
class pymc3.distributions.continuous.Exponential(lam, *args, **kwargs)
https://docs.pymc.io/api/distributions/continuous.html#pymc3.distributions.continuous.Exponential
\
Distributions.Exponential — Type.
https://juliastats.github.io/Distributions.jl/stable/univariate/#Distributions.Exponential
Exponentialのパラメトライズが違うことに気づかずにモデリングを行っていたのだが、Mambaで使っているDistiribution.jlの Exponential(θ) をPyMCの pm.Exponential(lam) と 同じ分布となるためには θ=1/lam とする必要がある。これを間違えていたため下のように事前分布が全く異なってしまい収束しなくなってしまっていた。
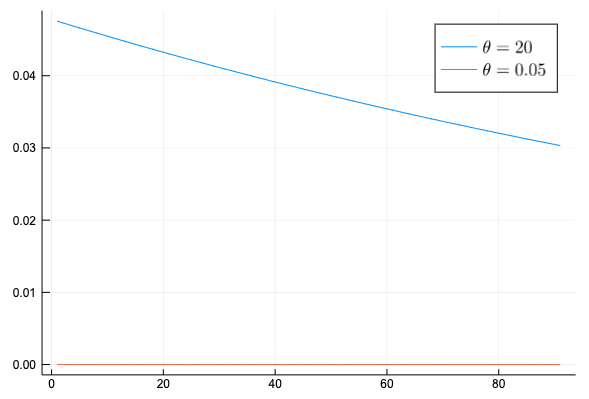
Mambaでモデルを作成すると次のようになる。パラメトライズの方法が違うので、変数は α の代わりに θ を使った。
model1 = Model(
obs = Stochastic(1,
(lambda, N) ->
UnivariateDistribution[
Poisson(lambda[i]) for i in 1:N],
false
),
lambda = Logical(1,
(lambda1, lambda2, tau, N) ->
(out = fill(lambda1, N);
i = Int64(tau.value) + 1; # Juliaは1-indexingのため
out[i:end, :] .= lambda2;
out),
),
lambda1 = Stochastic(theta -> Exponential(theta)),
lambda2 = Stochastic(theta -> Exponential(theta)),
tau = Stochastic(N -> DiscreteUniform(0, N)),
)
観察されるデータと θ を準備する。θ はメッセージ数の平均の逆数 α の逆数なので、メッセージ数の平均。
theta = mean(count_data.messages)
data0 = Dict{Symbol, Any}(
:obs => count_data.messages,
:theta => theta,
:N => length(count_data.messages),
)
初期値は下のようにする。今回はサンプリングのパスを3つとするので初期値も3つ用意する。
inits1 = [
Dict{Symbol, Any}(
:obs => count_data.messages,
:lambda1 => theta,
:lambda2 => theta,
:tau => 1,
) for _ in 1:3
]
サンプリングの設定では、 \( \tau \) は離散値なので DGS を使う。
scheme1 = [AMWG([:lambda1, :lambda2], 1.0), DGS(:tau)]
サンプリングを行うと、本文と同様、44, 45日後にユーザーが振る舞いを変えたというところの確率密度が高くなっている。離散値になっていないので、何か設定が間違っているのかもしれない。
setsamplers!(model1, scheme1)
sim1 = mcmc(model1, data0, inits1, 40000, burnin = 10000, thin = 3, chains = 3)
p1 = Mamba.plot(sim1[:, [:tau, :lambda1, :lambda2], :], legend = true)
Mamba.draw(p1, nrow = 3, ncol = 2)
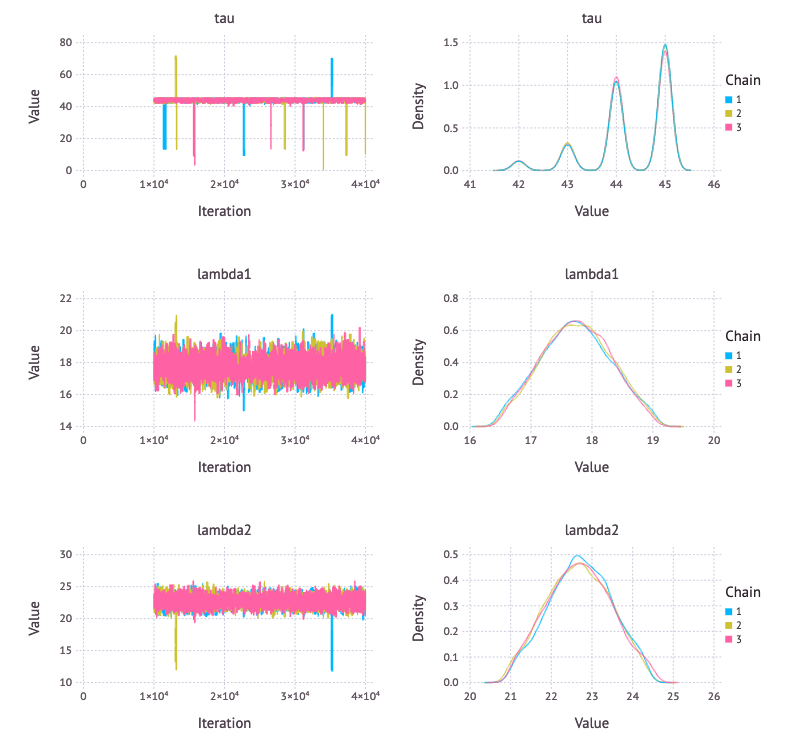
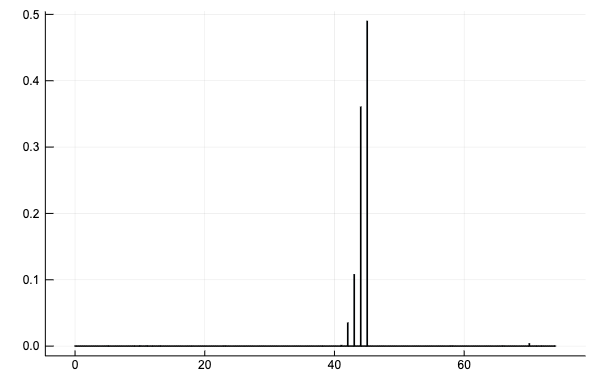
\( \tau \) のヒストグラムを確認すると、正しくサンプリングできているようだ。
histogram(vec(sim1[:, :tau, :].value), normalize = :probability, title = "tau", label = "")
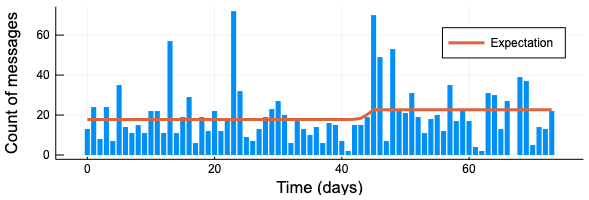
受信メッセージ数と期待値を表示する。
bar(0:N-1, count_data.messages, label = "", size = [600, 200],
linecolor = :transparent,
xlabel = "Time (days)", ylabel = "Count of messages")
plot!(0:N-1, vec(mean(sim1[:, :lambda, :].value, dims=[1, 3])), linewidth = 3, label = "Expectation")