前回に引き続き、「Pythonで体験するベイズ推論」をJuliaでやってみる。本に従い、前回作成した「メッセージ数に変化はあるか?」を二つの変化点の場合に拡張する。
変化点が二つの場合を考えてみる。モデルは変化点が一つの場合とほぼ同じで、
model2 = Model(
obs = Stochastic(1,
(lambda, N) ->
UnivariateDistribution[Poisson(lambda[i]) for i in 1:N],
false
),
lambda = Logical(1,
(lambda1, lambda2, lambda3, tau1, tau2, N) ->
(out = fill(lambda1, N);
i1 = Int64(tau1.value) + 1; # Juliaは1-indexingのため
i2 = Int64(tau2.value) + 1;
out[i1:end] .= lambda2;
out[i2:end] .= lambda3;
out),
false,
),
lambda1 = Stochastic(theta -> Exponential(theta)),
lambda2 = Stochastic(theta -> Exponential(theta)),
lambda3 = Stochastic(theta -> Exponential(theta)),
tau1 = Stochastic(N -> DiscreteUniform(0, N-1)),
tau2 = Stochastic((tau1, N) -> DiscreteUniform(tau1, N)),
)
初期値とサンプリングスキームを同様に与えてサンプリングすると、
inits2 = [
Dict{Symbol, Any}(
:obs => count_data.messages,
:lambda1 => theta,
:lambda2 => theta,
:lambda3 => theta,
:tau1 => 1,
:tau2 => N,
) for _ in 1:3
]
scheme2 = [AMWG([:lambda1, :lambda2, :lambda3], 1.0), DGS([:tau1, :tau2])]
setsamplers!(model2, scheme2) sim2 = mcmc(model2, data0, inits2, 40000, burnin = 10000, thin = 3, chains = 3)
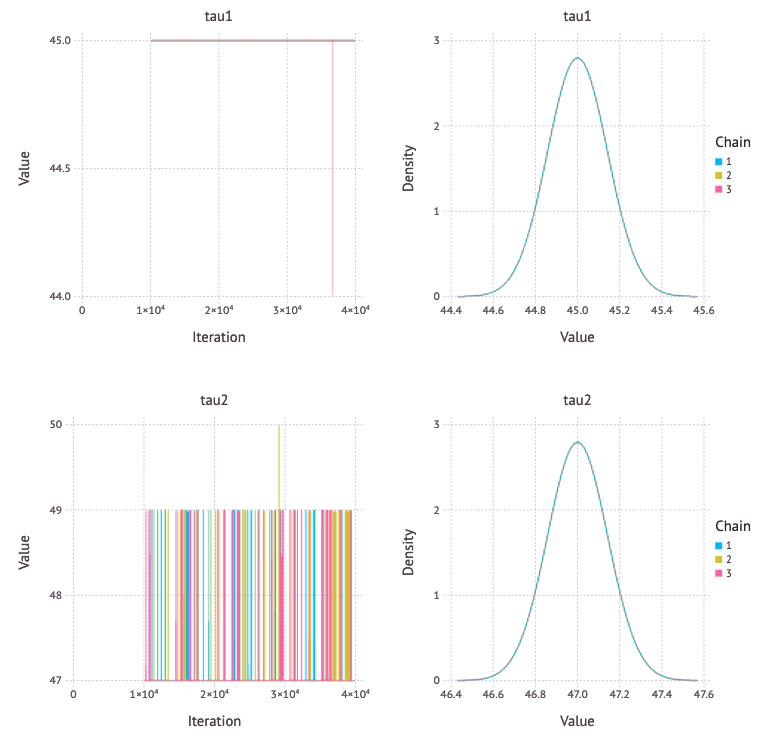
事後分布は以下のようになる。
p2 = Mamba.plot(sim2[:, [:tau1, :tau2], :], legend = true)
Mamba.draw(p2, nrow = 2, ncol = 2)
p2 = Mamba.plot(sim2[:, [:lambda1, :lambda2, :lambda3], :], legend = true)
Mamba.draw(p2, nrow = 3, ncol = 2)
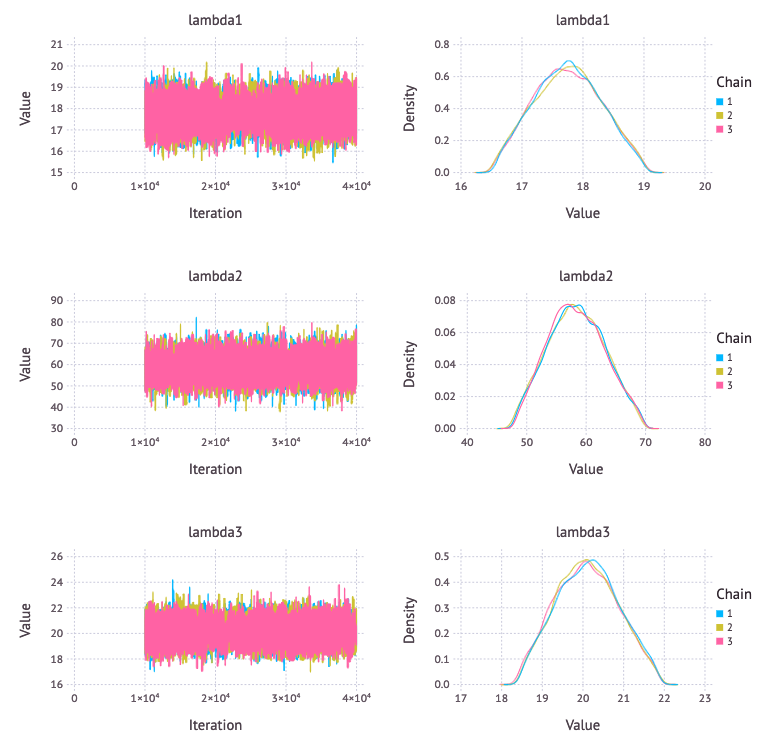
本で言及されていた、変化点の個数についても事前分布を作ってモデリングしてみたがうまくいかなかった。