「Pythonで体験するベイズ推論」の「2.2.7 例題 カンニングした学生の割合」をやってみよう。
学生が試験中にカンニングする頻度を求めたい。観測データは個人がカンニングしたかどうかは特定できない、以下のアルゴリズムを用いる。
- コイントスを(こっそり)行い、表が出たら正直に答える
- 裏が出た場合、もう一枚コインを(こっそり)投げ、表が出たら「カンニングした」と答え、裏が出たら「カンニングしなかった」と答える。
カンニングが全くなければ、「カンニングした」という回答がある確率は 1/2 * 1/2 = 1/4, 全員カンニングしていれば 1/2 + 1/2 * 1/2 = 3/4 になる。
まずはライブラリをインポート。
using Distributed
addprocs(3)
@everywhere using Mamba
using Plots
学生の数が100人、「カンニングした」という回答が35人とする。
N = 100
X = 35
Mambaのモデルは次のようになる。
model = Model(
obs = Stochastic(
(proportion, N) -> Binomial(N, proportion),
false
),
proportion = Logical(
(true_answers, first_coin_flips, second_coin_flips) ->
(observed = @.(first_coin_flips * true_answers + (1 - first_coin_flips) * second_coin_flips);
mean(observed)),
false
),
true_answers = Stochastic(1, p -> Bernoulli(p), false),
first_coin_flips = Stochastic(1, () -> Bernoulli(0.5), false),
second_coin_flips = Stochastic(1, () -> Bernoulli(0.5), false),
p = Stochastic(() -> Uniform()),
)
proportionを計算するときの
observed = @.(first_coin_flips * true_answers + (1 - first_coin_flips) * second_coin_flips)
は@マクロを使った書き方で、
observed = first_coin_flips .* true_answers .+ (1 .- first_coin_flips) .* second_coin_flips)
と同じである。 true_answers , first_coin_flips , second_coin_flips は長さNの Stochastic ベクターだが、Nをモデルに与えなくても、Stochastic コンストラクタの第1引数を1(1次元)にして、初期値に長さNのベクターを与えれば大丈夫。
data = Dict{Symbol, Any}(
:obs => X,
:N => N,
)
inits = [
Dict{Symbol, Any}(
:obs => X,
:proportion => 0.5,
:true_answers => rand(Bernoulli(), N),
:first_coin_flips => rand(Bernoulli(), N),
:second_coin_flips => rand(Bernoulli(), N),
:p => rand(Uniform()),
) for _ in 1:3
]
true_answers , first_coin_flips , second_coin_flips は \( \{0, 1\} \) からのサンプリングなので、Sampling Functionsを見ると BHMC, BIA, BMC3, BMGのどれかを使えば良いようである。BIA, BMC3, BMGを使って比較してみた。
BIAのサンプリング設定は下の通り。BMC3, BMG も scheme だけ変えればよく同様である。
samplings = 100000
burning = 20000
scheme_bia = [NUTS(:p), BIA([:true_answers, :first_coin_flips, :second_coin_flips])]
setsamplers!(model, scheme_bia)
sim_bia = mcmc(model, data, inits, samplings, burnin = burning, thin = 10, chains = 3)
p_bia = reshape(Mamba.plot(sim_bia, [:trace, :density, :autocor, :mean], legend = true), (2, 2))
Mamba.draw(p_bia, nrow = 2, ncol = 2)
BIA
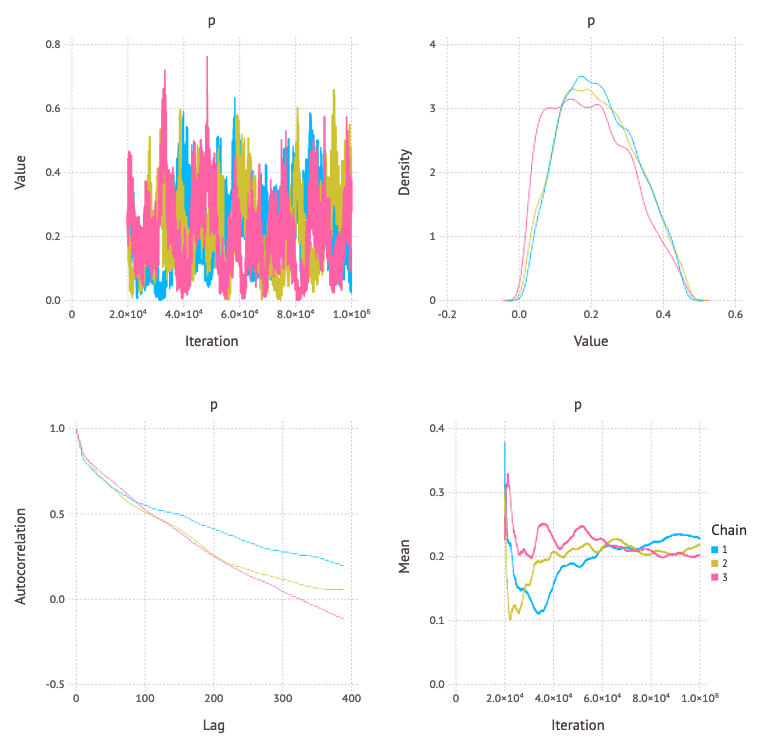
BMC3
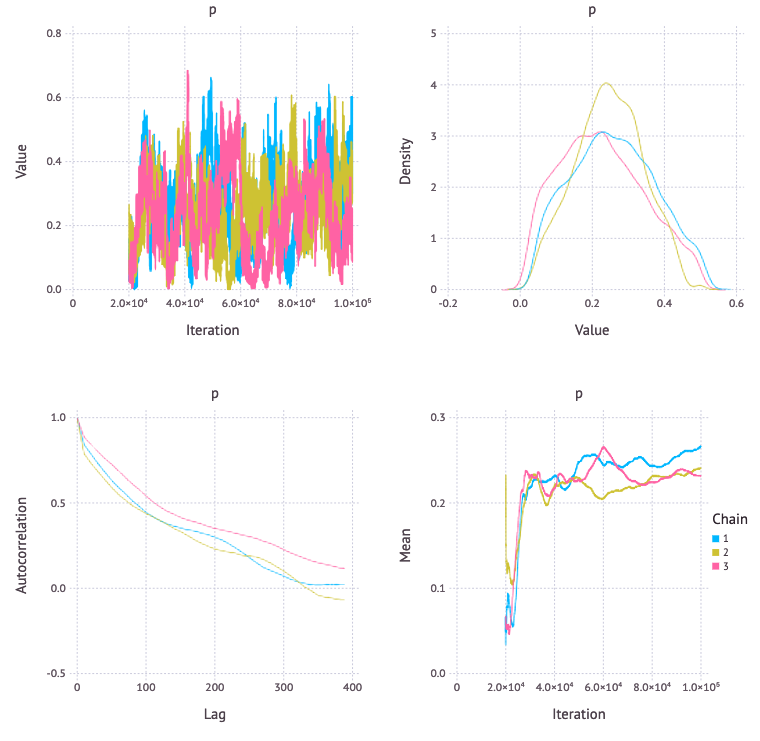
BMG
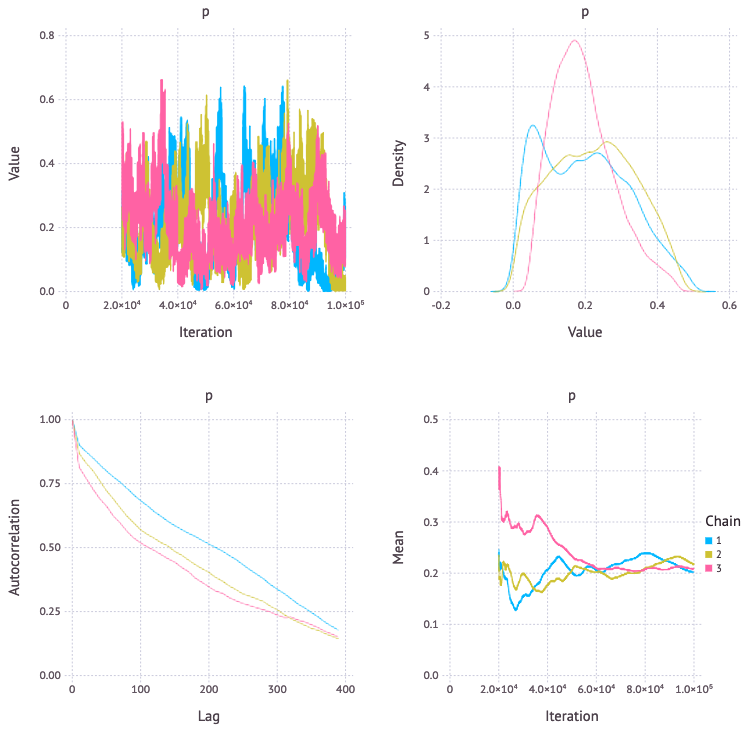
自己相関や確率密度を見ると BIA, BMC3 が良さそう。
もう一つのモデル
「カンニングしました」と答える確率は p/2 + 1/4 なので、proportion を計算する代わりにこれを直接使ってモデリングすることもできる。
another_model = Model(
obs = Stochastic(
(p, N) ->
(p_skewed = 0.5 * p + 0.25;
Binomial(N, p_skewed)),
false
),
p = Stochastic(() -> Uniform()),
)
another_scheme = [NUTS(:p)]
setsamplers!(another_model, another_scheme)
another_sim = mcmc(another_model, data, inits, samplings, burnin = burning, thin = 10, chains = 3)
another_p = reshape(Mamba.plot(another_sim, [:trace, :density, :autocor, :mean], legend = true), (2, 2))
Mamba.draw(another_p, nrow = 2, ncol = 2)
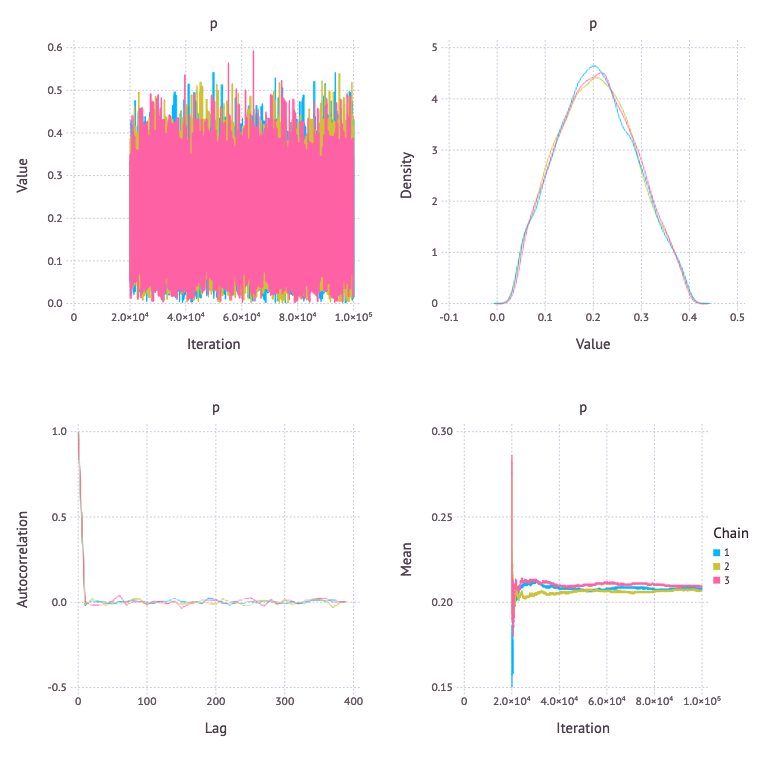
true_answers, first_coin_flips, second_coin_flips をモデリングした場合に比べて、収束が大きく向上している。