「データ解析のための統計モデリング入門」第11章の空間構造のある階層ベイズモデルに挑戦する前に、まずPyMC3のIntrinsic Gaussian ModelのサンプルをMambaで実装した。

https://github.com/matsueushi/lip_stick_mamba

参考にしたMatrix Multiplicationを用いたPyMC3の実装:

https://docs.pymc.io/notebooks/PyMC3_tips_and_heuristic.html#PyMC3-implementation-using-Matrix-multiplication

PyMCのモデル

with pm.Model() as model3:
    # Vague prior on intercept and effect
    beta = pm.Normal('beta', mu=0.0, tau=1.0, shape=(2, 1))

    # Priors for spatial random effects
    tau = pm.Gamma('tau', alpha=2., beta=2.)
    alpha = pm.Uniform('alpha', lower=0, upper=1)
    phi = pm.MvNormal('phi', mu=0, 
            tau=tau*(D - alpha*W), shape=(1, N))

    # Mean model
    mu = pm.Deterministic('mu', 
                    tt.exp(tt.dot(X, beta) + phi.T + log_offset))

    # Likelihood
    Yi = pm.Poisson('Yi', mu=mu.ravel(), observed=O)

    trace3 = pm.sample(3e3, cores=2, tune=1000)

は、Mambaだと下のようになる。PyMCとMambaで分布を指定するときに使うDistribution.jlではMvNormalのパラメーターの持ち方が違うことに注意。PyMCのMvNormalに該当するDistibution.jlの分布は 、MvNormalではなくMvNormalCanon。

car_model = Model(
    beta0 = Stochastic(() -> Normal()),
    beta1 = Stochastic(() -> Normal()),
    
    tau = Stochastic(() -> Distributions.Gamma(2.0, 0.5)),
    alpha = Stochastic(() -> Uniform()),
    phi = Stochastic(1,
        (tau, alpha, N, D, W) 
            -> MvNormalCanon(zeros(N), tau * (D - alpha * W)),
    ),
    
    mu = Logical(1, 
        (beta0, beta1, zscore_aff, phi, log_offset) -> 
        exp.(beta0 .+ beta1 .* zscore_aff .+ phi .+ log_offset)
    ),
    
    y = Stochastic(1,
        (mu, N) -> 
            UnivariateDistribution[Poisson(mu[i]) for i in 1:N],
        false
    )
)

サンプリングに関しては、NUTSが遅すぎるのでAWMGを使った。

car_scheme = [
    AMWG([:beta0, :beta1, :phi], 1.0), 
    Slice(:alpha, 1.0),
    Slice(:tau, 10.0),
]
setsamplers!(car_model, car_scheme)
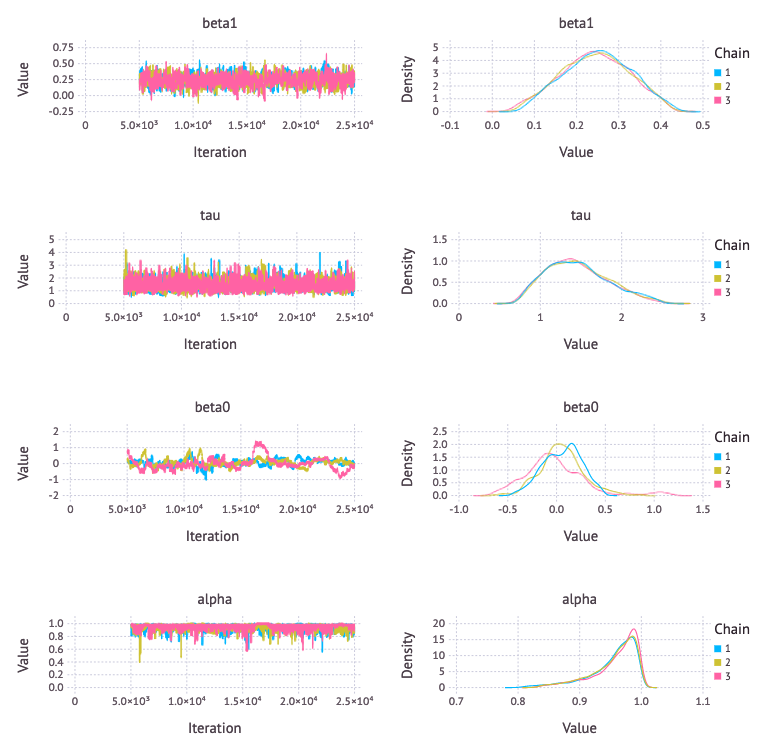
car_sim = mcmc(car_model, car_data, car_inits, 21000, 
                burnin = 1000, thin = 10, chains = 3)

CAR1

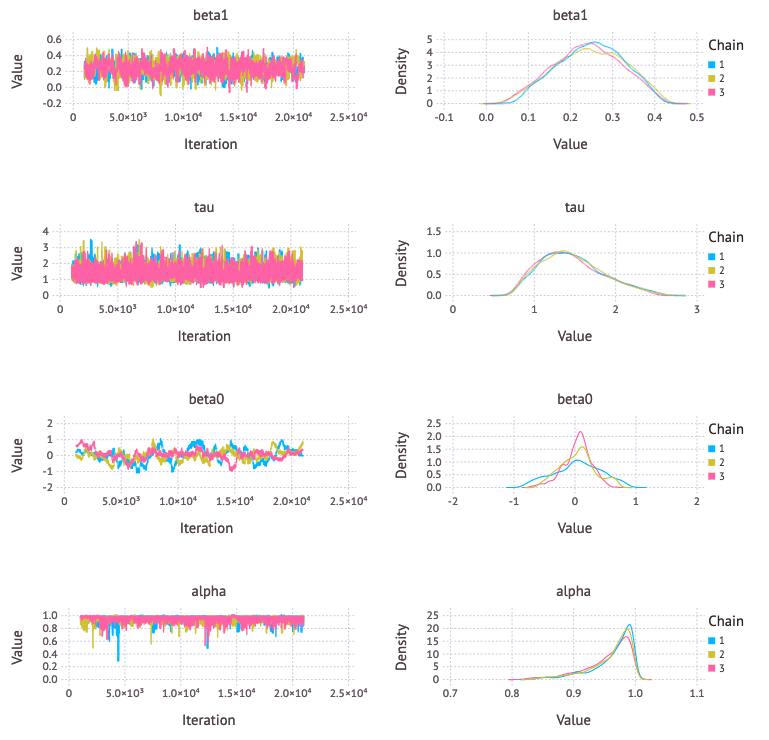
PyMCの場合とおおよそ同じ分布になったが、beta0 の収束がやや微妙な気がする。

サンプリング方法を下のように変更してもbeta0の収束はあまり良くならない。何か良い方法はあるのだろうか。

car_scheme = [
 AMWG([:alpha, :beta0], 1.0), 
 AMWG([:beta1, :phi], 0.1), 
 Slice(:tau, 10.0),
]
setsamplers!(car_model, car_scheme)
car_sim = mcmc(car_model, car_data, car_inits, 25000, burnin = 5000, thin = 10, chains = 3)

CAR2